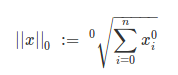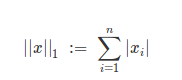在线性代数,函数分析等数学分支中,范数(Norm)是一个函数,是赋予某个向量空间(或矩阵)中的每个向量以长度或大小的函数。对于零向量,令其长度为零。直观的说,向量或矩阵的范数越大,则我们可以说这个向量或矩阵也就越大。有时范数有很多更为常见的叫法,如绝对值其实便是一维向量空间中实数或复数的范数,而Euclidean距离也是一种范数。
范数的一般化定义:设p≥1的实数,p-norm定义为:
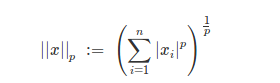
注意:范数是绝对值的p次方,不是本身的p次方
L0 范数:
L1 范数:
L2 范数:
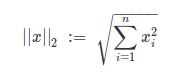
也叫Euclidean Norm(欧几里德范数),如果用于计算两个向量之间的不同,即是Euclidean Distance。